I chose this activity as one of my “New Discoveries” because it demonstrates that engaging in math responses is unique to each individual. It also highlights the fact that math problems can be approached in various ways. It clarified many of the “Big Ideas”, such as communicating math processes and the idea that math is unique to each individual. Additionally, it allowed me to reflect on my own approach to the question and connect it to other areas of learning.

What did I learn while completing the Small Number Investigation? Firstly, I gained knowledge on low floor, high ceiling questions. What are these? For more detail, take a look at the image I’ve included below from my investigation assignment:

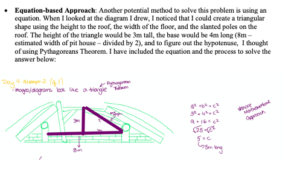
Click on the image to see it more clearly!

In summary, low floor, high ceiling questions allow for numerous possibilities in which learners can approach the question, and the answers can range depending on the learner’s comfort level. The Small Number Investigation demonstrated this clearly. There were so many ways to approach the questions, whether that be a more mathematical approach with equations (such as the Pythagorean Theorem), or a logical approach by considering the First Peoples historical background. Through taking time to think of various potential answers for the question, I was able to understand that math is not solely about the final answer, but more importantly the process to reach the answer. I’ve included some images from my investigation assignment that demonstrate various ways the questions can be approached. For these examples, I was solving the question “Why did Small Number think that the posts to build the rood were about 5m long each?”

Click on the image to make it bigger!

Click on the image to make it bigger!

While completing the investigation, I found it difficult to accept that the question was so open-ended and there was not a specific answer to the problem. This was strange to me, as my previous perception of math was that the answers were either right or wrong, and there is only one answer. However, this question proved to me that math is not about the answer, but about the process. It is important to emphasize this to students so they do not think that there is only one way to solve a math problem.

To address this challenge, I approached the problem with various strategies. By using numerous mathematical processes, I was able to see the importance of the process to reach the final answer. Thus, I was not focused on the final answer, but rather the strategies I used to reach my conclusion. Here is a list of some strategies I used to solve the problem:

  • Estimation
  • Comparison
  • Equation-based Approach
  • Existing Knowledge and Imagination
  • Trial and Error

Another challenge I had while working on this assignment was I did not know where to start! Since the question was so open-ended, I had a difficult time getting started and figuring out different strategies to approach the problem. To address this challenge, I focused on the incubation effect, which means re-visiting a problem multiple times over a few days. Each time a re-visited the problem, I was able to consider another way to approach it!

When I think of the incubation effect, I think of a light bulb! If you keep thinking about a problem, the lightbulb in your brain will eventually come on! (Photo by Christian Dubova on Unsplash).

Overall, I really enjoyed the process of completing the Small Number Investigation and I gained an abundance of knowledge that I will bring with me into my future classroom!